How Can I Play Sudoku? Examine Easy, Medium, and Hard Level Tips & Tricks.

How to play sudoku: This is a detailed tutorial for novices on how to solve sudoku. You will become an expert at completing easy, medium, and difficult Sudoku puzzles with the help of these ten Sudoku strategies.
Sudoku Solver Tips: Suduko, a difficult yet rewarding brain puzzle game, is among the most played worldwide. The printed version of Sudoku must have been familiar to all of us from publications and newspapers.
French newspapers began publishing Sudoku under the title Number Place. After being released by the Japanese puzzle manufacturer Nikoli in 1986 under the title Sudoku, which translates to “Single Number,” it became well-known. Sudoku was featured in a newspaper in 2004.
Sudoku: What is it?
Sudoku is a combinatorial number-placement problem that relies on logic. The goal of traditional Sudoku is to fill a 9×9 grid with numbers so that every row, every column, and each of the nine 3×3 subgrids that make up the grid (also known as “boxes,” “blocks,” or “regions”) has every number from 1 to 9.
Sudoku puzzles can be easy, medium, hard, or very hard in difficulty. The more pre-filled numbers there are in the grids, the easier the problem. There are less pre-filled numbers in the grids for puzzles that are harder.
You must carefully consider where to put each number in the game of Sudoku, which tests your ability to reason and use logic. You must be able to recognise patterns and draw conclusions, but no calculations or mathematical procedures are required. Playing sudoku is a terrific method to sharpen your mind. Your ability to focus, remember things, and solve problems can all be enhanced by it. It’s a terrific way to unwind and relieve tension, and it can also be a lot of fun.link
Let us Solve a Sudoku
To demonstrate how to solve a Sudoku puzzle, we will solve the rows, columns, and grids for a1 to i1, a2 to i2, and a3 to i3.
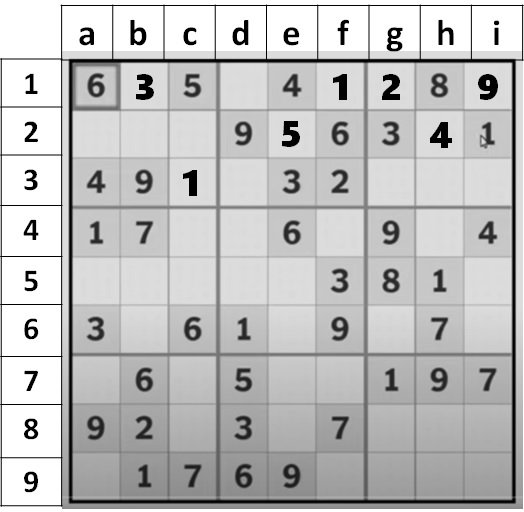
- The a1 to i3 grids are where we start. We have a 1 in i2 and a 2 in f3 after going through the rows and columns. We shall thus wait and proceed. Now that we know that g2 and e3 both have threes, we conclude that c3, c2, b2, and a2 are unable to have threes. We therefore entered 3 in the b1 cell.
- Next, we see that 31 and A3 both have a 4. Thus, g1, i1, g3, h3, and i3 are all unable to have a 4. Therefore, we set the h2 cell to a 4.
- Next, we see that our cell is a 5 in c1. We don’t see another of it, though. So we continue. Then we see a 6 in cell a1 and another 6 in cell f2. Thus, with the same reasoning as before, we determine that g1, i1, and h2 cannot contain a 6. Thus, the g3, h3, and i3 cells still have the potential to receive a 6. Since there are no sixes in the surrounding columns, we leave it open as a possibility and proceed.
- We then only have an 8 in h1 cell. Let’s go on to a 9 in d2 and another 9 in b3. We thus take use of this. This informs us that g3, h3, i3, and h2 cells cannot contain a 9. The only option left to us is a 9 in either g1 or i1 cells. Further column-wise analysis reveals a 9 in the g4 and h7 cells. We can then conclude that a 9 cannot be put in the g1 cell. We will therefore enter 9 in the i1 cell.
So far, our Sudoku looks like this:
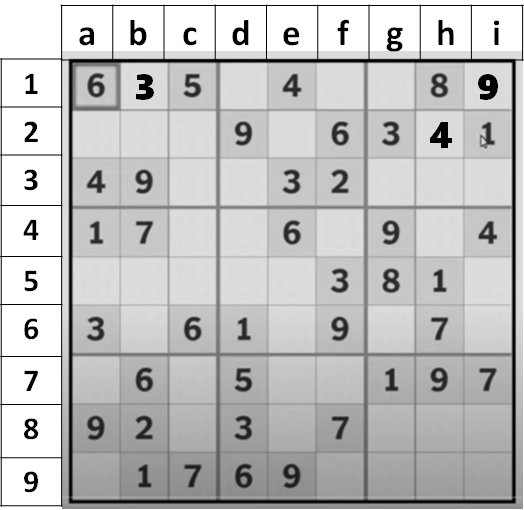
- Next, we review the numbers 1 through 9. The presence of a 2 in f3 cell is now visible. Since there is already a 2 in the 3×3 grid of d to f cells and g2, h2, and i2 cells are filled, we can now scan the rows and columns once more and see that there is a chance that there will be another 2 in the a2, b2, and c2 cells.
- Therefore, we conclude that a 2 can only be placed in a2 or c2 cells after scanning across and noticing that there is a 2 in the b8 cell. As we proceed, we determine that there is 1 in i2. We find a 1 in the a4 and d6 cells after additional scanning. As a result, we removed cells A1, D3, and E2 in order to insert a 1. The 1 will be placed in the f1 cell.
- Then, we see that c1 cell has a 5, hence d1, f1, and g1 cannot have a 5. Since e2 remains after elimination, we place a 5 in the e2 cell while maintaining the possibility of a 5 in the g3, h3, and i3 cells.
Now, our Sudoku looks like this:
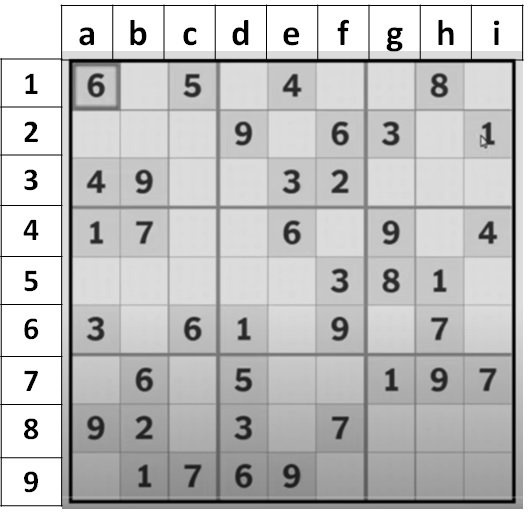
- Only one candidate, a 7, is absent from cell d1 in cells a1 through i1. Furthermore, since we can see a 7 in the h6 and i7 cells, a 7 will also appear in the g3 cell. Since there is already an 8 in the h1 cell and the a3, b3, and c3 cells are already full, we conclude that an 8 cannot go in the g3. We therefore entered an 8 in the d3 cell.
- We can now determine the last seven since we have already determined that a 7 is in d1 and a 7 in g3. There is a 7 in cell b4 and another 7 in cell c9, as may be seen by scanning. Therefore, we can place the final seven in an a2 cell using the elimination procedure.
- Going back to the other two, we can see that the b8 cell has a 2, thus the c2 cell is what’s left. In the c2 cell, we entered a 2. We may now fill up the b2 cell with the final possibility, an 8. The h3 and i3 cells are now all that remain. Only until the remaining rows, columns, and grids have been solved can these two cells be determined.
We shall share the solved Sudoku puzzle here for you to learn and practice.




